Point Estimate Evaluation

After training a model and preparing predictions, EquiBoots can be used to evaluate how your model performs across different demographic groups. The most basic step in this process is calculating point estimates. These are performance metrics for each group without resampling or bootstrapping.

EquiBoots supports the computation of group-specific and overall point estimates for performance metrics across classification and regression tasks. These estimates form the basis for fairness auditing by revealing how models perform across different subpopulations or sensitive attributes.

The binary classification examples of this section demonstrate how to compute group-wise performance metrics using model outputs and fairness variables from the Adult Income dataset [1]. For bootstrapped confidence intervals, refer to the bootstrapped metrics evaluation section.

Supported Metrics

For classification tasks, the following metrics are supported:

Accuracy, Precision, Recall, F1-score
AUROC, AUPRC (for probabilistic models)
Calibration Area Under The Curve
Log Loss, Brier Score

For regression tasks:

\(R^2, MAE, MSE, RMSE\)
Group-based residual plots

Initial Set-up

Step 1: Import and Initialize EquiBoots

To begin, we instantiate the EquiBoots class with the required inputs: the true outcome labels (y_test), predicted class labels (y_pred), predicted probabilities (y_prob), and a DataFrame that holds sensitive attributes like race or sex.

Note

y_pred, y_prob, y_test are defined inside the modeling generation section.

Once initialized, EquiBoots uses its internal grouping mechanism to enable fairness auditing by slicing the dataset into mutually exclusive subgroups based on each fairness variable. This slicing is a prerequisite for evaluating model behavior across subpopulations.

The grouper method stores index-level membership for each group, ensuring that only groups meeting a minimum sample size are considered. This prevents unstable or misleading metric calculations. Once sliced, we call slicer to extract the y_true, y_pred, and y_prob values corresponding to each group. Finally, get_metrics is used to compute core performance metrics for each subgroup.

import equiboots as eqb

# Create fairness DataFrame
fairness_df = X_test[['race', 'sex']].reset_index()

eq = eqb.EquiBoots(
    y_true=y_test,
    y_prob=y_prob,
    y_pred=y_pred,
    fairness_df=fairness_df,
    fairness_vars=["race", "sex"],
)

Step 2: Slice Groups and Compute Point Estimates

Once the class is initialized, we slice the dataset into subgroups and compute performance metrics for each group. This step is critical for assessing whether model performance varies by group.

import equiboots as eqb

sliced_race_data = eq.slicer("race")
race_metrics = eq.get_metrics(sliced_race_data)

sliced_sex_data = eq.slicer("sex")
sex_metrics = eq.get_metrics(sliced_sex_data)

Each output is a dictionary of group names (e.g., 'Male', 'Female', 'Asian', 'White') mapped to performance metrics such as accuracy, AUROC, precision, or RMSE, depending on the task type.

Metrics DataFrame

Because these dictionaries can contain many entries and nested metric structures, we avoid printing them directly in documentation. Instead, we use the metrics_dataframe() function to transform the dictionary into a clean, filterable DataFrame.

To keep the table concise and relevant, we subset the DataFrame to include only a selected set of metrics:

Accuracy
Precision
Recall
F1 Score
Specificity
TP Rate
Prevalence
Average Precision Score
Calibration AUC

metrics_dataframe(metrics_data)

Transforms a list of grouped metric dictionaries into a single flat DataFrame.

Parameters:: metrics_data (List[Dict[str, Dict[str, float]]]) – A list of dictionaries, where each dictionary maps a group name to its associated performance metrics.
Returns:: A tidy DataFrame with one row per group and one column per metric. The group names are stored in the attribute_value column.
Return type:: pd.DataFrame

This function is used after computing metrics using eqb.get_metrics().

It flattens nested group-wise dictionaries into a readable table, enabling easy subsetting, filtering, and export.

Common use cases include displaying fairness-related metrics such as Accuracy, Precision, Recall, Specificity, Calibration AUC, and others across different sensitive attribute groups (e.g., race, sex).

The metrics_dataframe() function simplifies post-processing and reporting by converting the raw output of group-level metrics into a tabular format. Each row corresponds to a demographic group, and each column represents a different metric.

Below is an example of how this function is used in practice to format metrics by race:

import equiboots as eqb

race_metrics_df = eqb.metrics_dataframe(metrics_data=race_metrics)
race_metrics_df = race_metrics_df[
    [
        "attribute_value",
        "Accuracy",
        "Precision",
        "Recall",
        "F1 Score",
        "Specificity",
        "TP Rate",
        "Prevalence",
        "Average Precision Score",
        "Calibration AUC",
    ]
]
## round to 3 decimal places for readability
round(race_metrics_df, 3)

This yields a structured and readable table of group-level performance for use in reporting or further analysis.

Output

	attribute_value	Accuracy	Precision	Recall	F1 Score	Specificity	TP Rate	Prevalence	Calibration AUC
0	White	0.853	0.761	0.638	0.694	0.929	0.638	0.262	0.040
1	Black	0.931	0.861	0.549	0.670	0.987	0.549	0.128	0.054
2	Asian-Pac-Islander	0.826	0.760	0.543	0.633	0.934	0.543	0.277	0.140
3	Amer-Indian-Eskimo	0.879	0.444	0.364	0.400	0.943	0.364	0.111	0.323
4	Other	0.958	1.000	0.500	0.667	1.000	0.500	0.083	0.277

Statistical Tests

After computing point estimates for different demographic groups, we may want to assess whether observed differences in model performance are statistically significant. This is particularly important when determining if disparities are due to random variation or reflect systematic bias.

EquiBoots provides a method to conduct hypothesis testing across group-level metrics. The analyze_statistical_significance function performs appropriate statistical tests—such as Chi-square tests for classification tasks—while supporting multiple comparison adjustments.

analyze_statistical_significance(metric_dict, var_name, test_config, differences=None)

Performs statistical significance testing of metric differences between groups.

This method compares model performance across subgroups (e.g., race, sex) to determine whether the differences in metrics (e.g., accuracy, F1 score) are statistically significant. It supports multiple test types and adjustment methods for robust group-level comparison.

Parameters:

metric_dict (dict) – Dictionary of metrics returned by get_metrics(), where each key is a group name and values are metric dictionaries.
var_name (str) – The name of the sensitive attribute or grouping variable (e.g., "race", "sex").
test_config (dict) –
Configuration dictionary defining how the statistical test is performed. The following keys are supported:
- test_type: Type of test to use (e.g., "chi_square", "bootstrap").
- alpha: Significance threshold (default: 0.05).
- adjust_method: Correction method for multiple comparisons (e.g., "bonferroni", "fdr_bh", "holm", or "none").
- confidence_level: Confidence level used to compute intervals (e.g., 0.95).
- classification_task: Specify if the model task is "binary_classification" or "multiclass_classification".
differences (list, optional) – Optional precomputed list of raw metric differences (default is None; typically not required).

Returns:

A nested dictionary containing statistical test results for each metric, with each value being a StatTestResult object that includes:

test statistic
raw and adjusted p-values
confidence intervals
significance flags (True / False)
effect sizes (e.g., Cohen’s d, rank-biserial correlation)

Return type:

Dict[str, Dict[str, StatTestResult]]

Raises:

ValueError – If test_config is not provided or is None.

This function returns a dictionary where each key is a metric name and the corresponding value is another dictionary mapping each group to its StatTestResult.

Example

The following example demonstrates how to configure and run these tests on performance metrics for the race and sex subgroups:

test_config = {
    "test_type": "chi_square",
    "alpha": 0.05,
    "adjust_method": "bonferroni",
    "confidence_level": 0.95,
    "classification_task": "binary_classification",
}
stat_test_results_race = eq.analyze_statistical_significance(
    race_metrics, "race", test_config
)

stat_test_results_sex = eq.analyze_statistical_significance(
    sex_metrics, "sex", test_config
)

overall_stat_results = {
    "sex": stat_test_results_sex,
    "race": stat_test_results_race,
}

Statistical Significance Plots

EquiBoots supports formal statistical testing to assess whether differences in performance metrics across demographic groups are statistically significant.

When auditing models for fairness, it’s important not just to observe differences in metrics like accuracy or recall, but to determine whether these differences are statistically significant. EquiBoots provides built-in support for this analysis via omnibus and pairwise statistical tests.

Test Setup

EquiBoots uses chi-square tests to evaluate:
- Whether overall performance disparities across groups are significant (omnibus test).
- If so, which specific groups significantly differ from the reference (pairwise tests).

Reference groups for each fairness variable can be set manually during class initialization using the reference_groups parameter:

eq = eqb.EquiBoots(
    y_true=...,
    y_pred=...,
    y_prob=...,
    fairness_df=...,
    fairness_vars=["race", "sex"],
    reference_groups=["white", "female"]
)

Group Metrics Point Plot

eq_group_metrics_point_plot(group_metrics, metric_cols, category_names, include_legend=True, cmap='tab20c', save_path=None, filename='Point_Disparity_Metrics', strict_layout=True, figsize=None, show_grid=True, plot_thresholds=(0.0, 2.0), show_pass_fail=False, y_lim=None, leg_cols=3, raw_metrics=False, statistical_tests=None, show_reference=True, **plot_kwargs)

Creates a grid of point plots for visualizing metric values (or disparities) across sensitive groups and multiple categories (e.g., race, sex). Each subplot corresponds to one (metric, category) combination, and groups are colored or flagged based on significance or pass/fail criteria.

Parameters:

group_metrics (list[dict[str, dict[str, float]]]) – A list of dictionaries where each dictionary maps group names to their respective metric values for one category.
metric_cols (list[str]) – List of metric names to plot (one per row).
category_names (list[str]) – Names of each category corresponding to group_metrics (one per column).
include_legend (bool) – Whether to display the legend on the plot.
cmap (str) – Colormap used to distinguish groups.
save_path (str or None) – Directory path where the plot should be saved. If None, the plot is shown.
filename (str) – Filename for saving the plot (without extension).
strict_layout (bool) – Whether to apply tight layout spacing.
figsize (tuple[float, float] or None) – Tuple for figure size (width, height).
show_grid (bool) – Toggle for showing gridlines on plots.
plot_thresholds (tuple[float, float]) – A tuple (lower, upper) for pass/fail thresholds.
show_pass_fail (bool) – Whether to color points based on pass/fail evaluation rather than group color.
y_lim (tuple[float, float] or None) – Y-axis limits as a (min, max) tuple.
leg_cols (int) – Number of columns in the group legend.
raw_metrics (bool) – Whether the input metrics are raw values (True) or already calculated disparities (False).
statistical_tests (dict or None) – Dictionary mapping categories to their statistical test results, used for annotating groups with significance markers.
show_reference (bool) – Whether to plot the horizontal reference line (e.g., y=1 for ratios).
plot_kwargs (dict[str, Union[str, float]]) – Additional keyword arguments passed to sns.scatterplot.

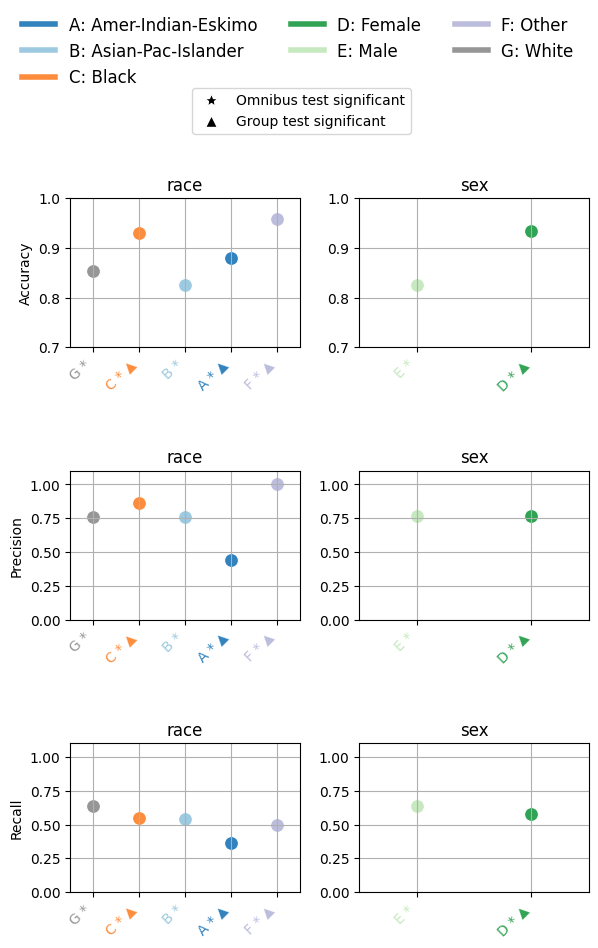
Once tests are computed, the eq_group_metrics_point_plot function can visualize point estimates along with statistical significance annotations:

eqb.eq_group_metrics_point_plot(
    group_metrics=[race_metrics, sex_metrics],
    metric_cols=[
        "Accuracy",
        "Precision",
        "Recall",
    ],
    category_names=["race", "sex"],
    figsize=(6, 8),
    include_legend=True,
    raw_metrics=True,
    show_grid=True,
    y_lim=(0, 1.1),
    statistical_tests=overall_stat_results,
    show_pass_fail=False,
    show_reference=False,
    y_lims = {(0,0): (0.70, 1.0), (0,1): (0.70, 1.0)}
)

Output

The chart above summarizes how model performance varies across race and sex groups for three key metrics: Accuracy, Precision, and Recall.

Each subplot corresponds to a single metric, plotted separately for race (left) and sex (right).

Here’s how to read the plot:

Each point shows the average metric score for a demographic group.
Letters (A–G) label the groups (e.g., A = Amer-Indian-Eskimo, B = Asian-Pac-Islander), with the full mapping provided in the legend.
The star symbol (★) below a group axis label indicates that the omnibus test for the corresponding fairness attribute (e.g., race or sex) was statistically significant overall.
The triangle symbol (▲) denotes groups that differ significantly from the reference group, as determined by pairwise statistical tests (e.g., Bonferroni-adjusted chi-square).
Color-coding helps distinguish categories and corresponds to the legend at the top.

This visualization reveals whether disparities exist not only numerically, but also statistically, helping validate whether observed group-level differences are likely due to bias or simply random variation.

Statistical Metrics table

Once statistical tests have been performed, we can summarize the results in a structured table that shows:

The performance metrics for each group.
Whether the omnibus test detected any significant overall differences.
Which individual groups differ significantly from the reference group.

This is done using the metrics_table function from EquiBoots, which takes in group metrics, test results, and the name of the reference group:

metrics_table(metrics, statistical_tests=None, differences=None, reference_group=None)

Parameters:

metrics (dict or list) – A dictionary or list of dictionaries containing metric results per group. This can either be point estimate output from get_metrics or bootstrapped results.
statistical_tests (dict, optional) – Output from analyze_statistical_significance containing omnibus and pairwise test results. If provided, annotations will be added to the output table to reflect significance.
differences (list of dict, optional) – A list of bootstrapped difference dictionaries returned from calculate_differences. If provided, the function will average these differences and annotate the results if significant.
reference_group (str, optional) – Name of the reference group used in pairwise comparisons. Only needed if displaying pairwise significance for bootstrapped differences.

Returns:

A pandas DataFrame where rows are metric names and columns are group names. If statistical_tests is provided: - Omnibus test significance is marked with an asterisk (*) next to column names. - Pairwise group significance (vs. reference) is marked with a triangle (▲).

Return type:

pd.DataFrame

Note

The function supports both point estimates and bootstrapped results.
When using bootstrapped differences, it computes the mean difference for each metric across iterations.
Automatically drops less commonly visualized metrics like Brier Score, Log Loss, and Prevalence for clarity if significance annotations are active.

from equiboots.tables import metrics_table

stat_metrics_table_point = metrics_table(
    race_metrics,
    statistical_tests=stat_test_results_race,
    reference_group="White",
)

You can then display the table as follows:

## Table with metrics per group and statistical significance shown on
## columns for omnibus and/or pairwise

stat_metrics_table_point

The resulting table displays one row per group and one column per metric. Symbols like * and ▲ appear in the appropriate cells to indicate significance:

★ marks metrics where the omnibus test found significant variation across all groups.
▲ marks metrics where a specific group differs significantly from the reference group.

This format provides a concise, interpretable snapshot of where disparities are statistically supported in your model outputs.

	White *	Black * ▲	Asian-Pac-Islander *	Amer-Indian-Eskimo * ▲	Other * ▲
Accuracy	0.853	0.931	0.826	0.879	0.958
Precision	0.761	0.861	0.76	0.444	1
Recall	0.638	0.549	0.543	0.364	0.5
F1 Score	0.694	0.67	0.633	0.4	0.667
Specificity	0.929	0.987	0.934	0.943	1
TP Rate	0.638	0.549	0.543	0.364	0.5
FP Rate	0.071	0.013	0.066	0.057	0
FN Rate	0.362	0.451	0.457	0.636	0.5
TN Rate	0.929	0.987	0.934	0.943	1
TP	1375	62	38	4	3
FP	432	10	12	5	0
FN	780	51	32	7	3
TN	5631	760	171	83	66
Predicted Prevalence	0.22	0.082	0.198	0.091	0.042

Group Curve Plots

To help visualize how model performance varies across sensitive groups, EquiBoots provides a convenient plotting function for generating ROC, Precision-Recall, and Calibration curves by subgroup. These visualizations are essential for identifying disparities in predictive behavior and diagnosing potential fairness issues.

The function below allows you to create either overlaid or per-group subplots, customize curve aesthetics, exclude small or irrelevant groups, and optionally save plots for reporting.

After slicing your data using the slicer() method and organizing group-specific y_true and y_prob values, you can pass the resulting dictionary to eq_plot_group_curves to generate interpretable, publication-ready visuals.

eq_plot_group_curves(data, curve_type='roc', n_bins=10, decimal_places=2, curve_kwgs=None, line_kwgs=None, title='Curve by Group', filename='group', save_path=None, figsize=(8, 6), dpi=100, subplots=False, n_cols=2, n_rows=None, group=None, color_by_group=True, exclude_groups=0, show_grid=True, lowess=0, lowess_kwargs=None, shade_area=False, plot_hist=False)

Plots ROC, Precision-Recall, or Calibration curves by demographic group. Supports overlaid and subplot layouts, optional smoothing with LOWESS, shaded areas, and histogram overlays for calibration curves.

Parameters:

data (Dict[str, Dict[str, np.ndarray]]) – Dictionary mapping group names to dictionaries containing y_true and y_prob arrays. Typically the output of eqb.slicer().
curve_type (str) – Type of curve to plot. Options are "roc", "pr", or "calibration".
n_bins (int) – Number of bins to use for calibration curves. Ignored for ROC and PR.
decimal_places (int) – Number of decimal places to show in curve labels (e.g., for AUC or Brier scores).
curve_kwgs (Dict[str, Dict[str, Union[str, float]]], optional) – Optional dictionary mapping group names to curve styling parameters (e.g., color, linestyle).
line_kwgs (Dict[str, Union[str, float]], optional) – Optional styling for the reference line (e.g., diagonal in ROC or calibration).
title (str) – Title of the entire figure.
filename (str) – Filename prefix for saving the figure (without file extension).
save_path (str or None) – Directory path where the figure will be saved. If None, the plot is only displayed.
figsize (Tuple[float, float]) – Tuple specifying the figure size in inches (width, height).
dpi (int) – Resolution of the output figure in dots per inch.
subplots (bool) – Whether to generate a subplot per group. If False, all curves are overlaid.
n_cols (int) – Number of columns in the subplot grid.
n_rows (int or None) – Number of rows in the subplot grid. If None, it’s inferred automatically.
group (str or None) – If set, plots only the specified group.
color_by_group (bool) – If True, assigns a different color to each group.
exclude_groups (Union[int, str, List[str], Set[str]]) – Optionally exclude specific groups by name or by minimum sample size.
show_grid (bool) – Whether to display background gridlines in the plots.
lowess (float) – Smoothing factor (0–1) for LOWESS calibration curves. Set to 0 to disable.
lowess_kwargs (Dict[str, Union[str, float]], optional) – Dictionary of additional styling arguments for LOWESS curves.
shade_area (bool) – Whether to fill the area beneath each curve (only for ROC and PR).
plot_hist (bool) – If True, displays a histogram of predicted probability counts beneath each calibration curve. Automatically enables subplots=True.

Returns:

None. Displays or saves the plot depending on the save_path argument.

Return type:

None

Note

When plot_hist=True, each subplot includes a histogram showing how many predictions fall into each predicted probability bin. This is especially useful for interpreting calibration performance in regions with dense or sparse predictions.
LOWESS smoothing is useful for non-linear calibration curves or small sample groups.
When subplots=False and group=None, all groups are overlaid on a single plot.
Setting both group and subplots=True will raise an error.

ROC AUC Curve

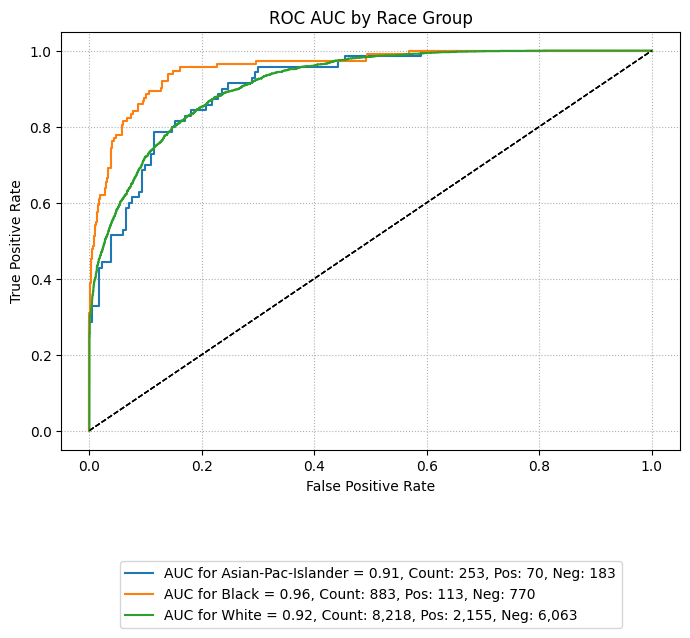
The following code generates an ROC AUC curve comparing performance across racial groups. This visualization helps assess whether the model maintains similar true positive and false positive trade-offs across subpopulations.

By setting subplots=False, the curves for each group are overlaid on a single plot, making disparities visually apparent. Groups with insufficient sample sizes or minimal representation can be excluded using the exclude_groups parameter, as shown below.

eqb.eq_plot_group_curves(
    sliced_race_data,
    curve_type="roc",
    title="ROC AUC by Race Group",
    figsize=(7, 7),
    decimal_places=2,
    subplots=False,
    exclude_groups=["Amer-Indian-Eskimo", "Other"]
)

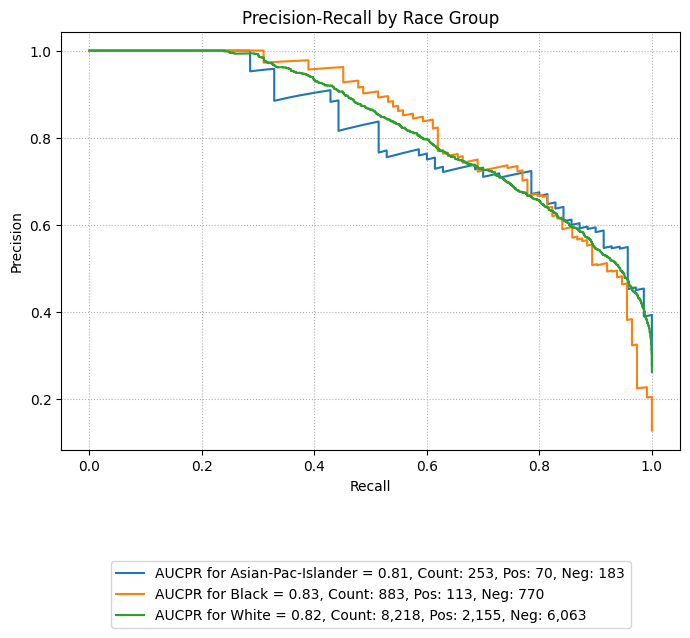
Precision-Recall Curves

eqb.eq_plot_group_curves(
    sliced_race_data,
    curve_type="pr",
    subplots=False,
    figsize=(7, 7),
    title="Precision-Recall by Race Group",
    exclude_groups=["Amer-Indian-Eskimo", "Other"]
)

Calibration Plots

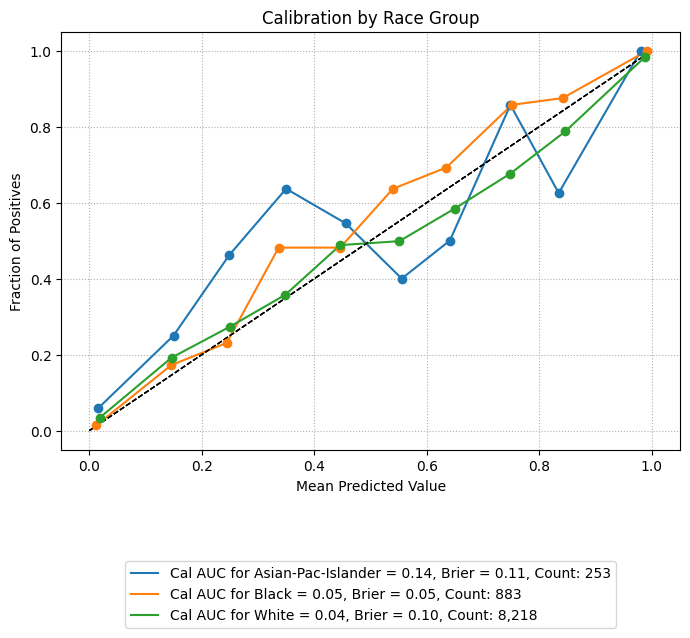
Calibration plots compare predicted probabilities to actual outcomes, showing how well the model’s confidence aligns with observed frequencies. A perfectly calibrated model will have a curve that closely follows the diagonal reference line.

The example below overlays calibration curves by racial group, using the same sliced data. Groups with low representation are excluded to ensure stable and interpretable plots.

For additional context on the geometric intuition behind calibration curves, including how the area between the observed curve and the ideal diagonal can be interpreted, see the Mathematical Framework section. That section illustrates how integration under the curve provides a mathematical view of calibration performance.

Example 1 (Calibration Overlay)

eqb.eq_plot_group_curves(
    sliced_race_data,
    curve_type="calibration",
    title="Calibration by Race Group",
    figsize=(7, 7),
    decimal_places=2,
    subplots=False,
    exclude_groups=["Amer-Indian-Eskimo", "Other"]
)

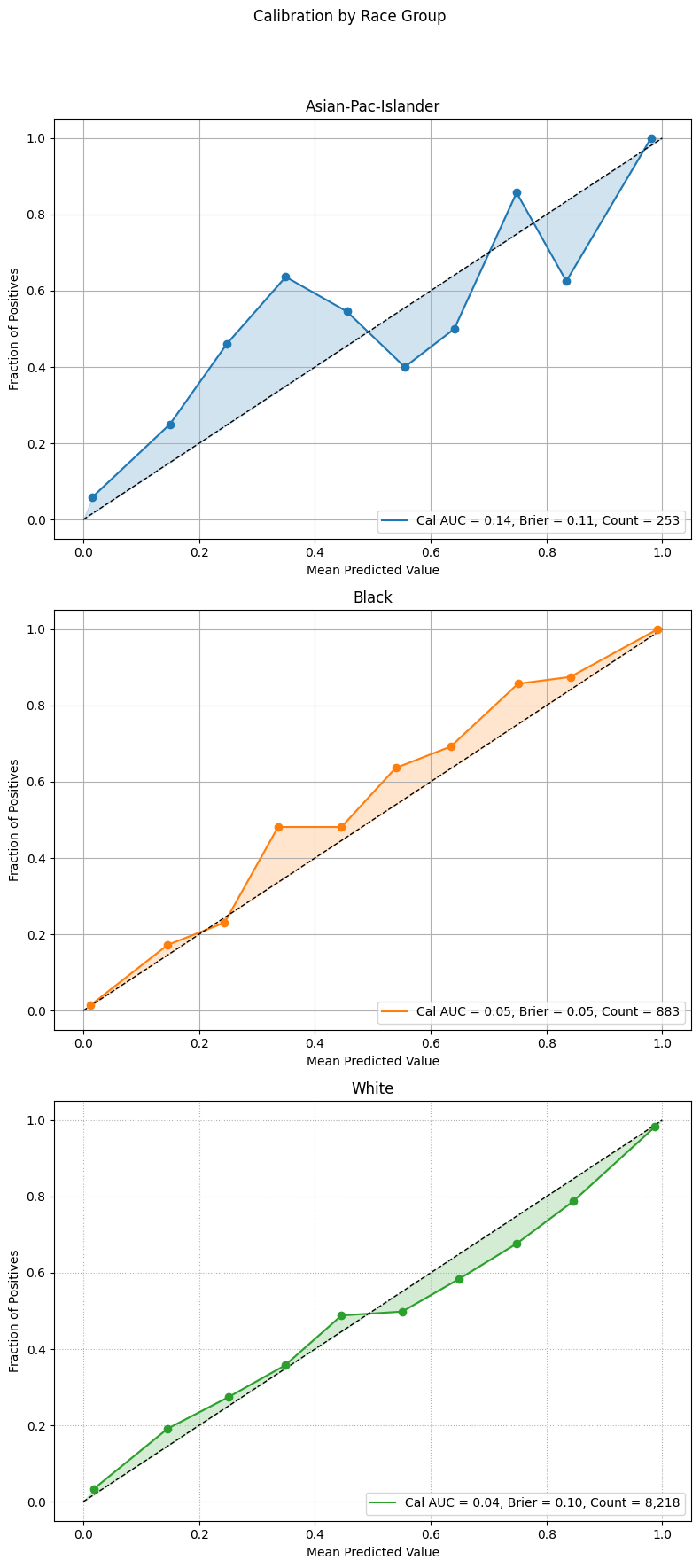
Example 2 (Calibration Subplots)

This example builds on the previous one by showing individual calibration curves in separate subplots and enabling shaded areas beneath the curves. This layout improves visual clarity, especially when comparing many groups or when the overlaid version appears cluttered.

Setting shade_area=True fills the area under each calibration curve. Subplots also help isolate each group’s performance, allowing easier inspection of group-specific trends.

eqb.eq_plot_group_curves(
    sliced_race_data,
    curve_type="calibration",
    title="Calibration by Race Group",
    figsize=(7, 7),
    decimal_places=2,
    subplots=True,
    shade_area=True,
    n_cols=3,
    exclude_groups=["Amer-Indian-Eskimo", "Other"]
)

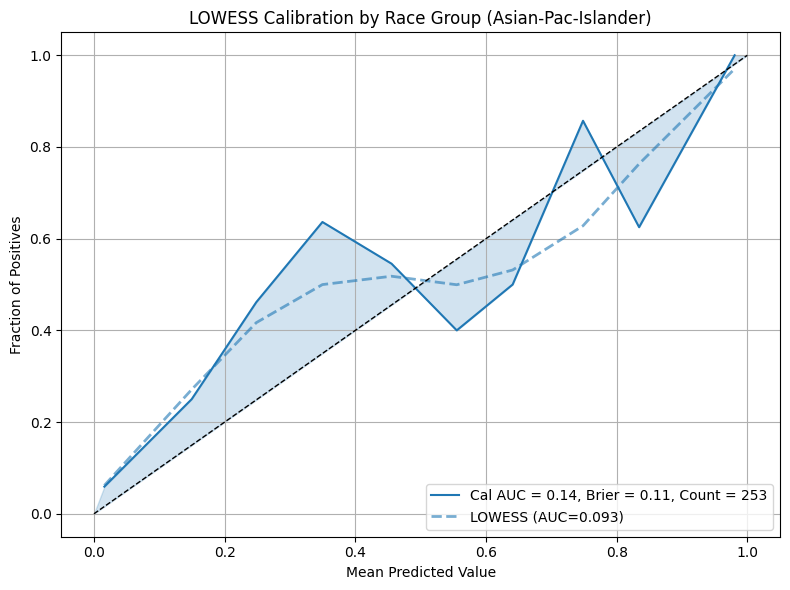
Example 3 (LOWESS Calibration)

This example demonstrates the use of Locally Weighted Scatterplot Smoothing (LOWESS) to fit a locally adaptive curve for calibration. This technique is helpful when calibration is non-linear or when jagged curves result from small group sizes or class imbalance.

Note

Enable LOWESS smoothing by setting the lowess parameter to a float between 0 and 1, which controls the smoothing span. Additional styling can be applied via lowess_kwargs.

eqb.eq_plot_group_curves(
    sliced_race_data,
    curve_type="calibration",
    title="Calibration by Race Group (LOWESS Smoothing)",
    figsize=(7, 7),
    decimal_places=2,
    subplots=True,
    lowess=0.6,
    lowess_kwargs={"linestyle": "--", "linewidth": 2, "alpha": 0.6},
    n_cols=3,
    exclude_groups=["Amer-Indian-Eskimo", "Other"]
)

LOWESS produces smoother and more flexible calibration curves compared to binning. It is particularly useful for identifying subtle trends in over or under-confidence across different segments of the population.

Example 4 (Calibration Histograms)

When plot_hist=True is enabled, the function displays a histogram of sample counts beneath the calibration curve for each group. Each bar shows how many predictions fall into a given probability bin (e.g., 0.0–0.1, 0.1–0.2). This is helpful for diagnosing whether calibration differences occur in well-populated regions of the probability spectrum or in sparse areas with few predictions.

Note

Histograms are especially useful when interpreting overconfident or underconfident predictions across different groups. Regions with sparse histogram bars may also indicate model uncertainty or data scarcity in those probability intervals.

eqb.eq_plot_group_curves(
    sliced_race_data,
    curve_type="calibration",
    title="Calibration by Race Group",
    n_bins=10,
    show_grid=False,
    exclude_groups=["Amer-Indian-Eskimo", "Other"]
    plot_hist=True,

)

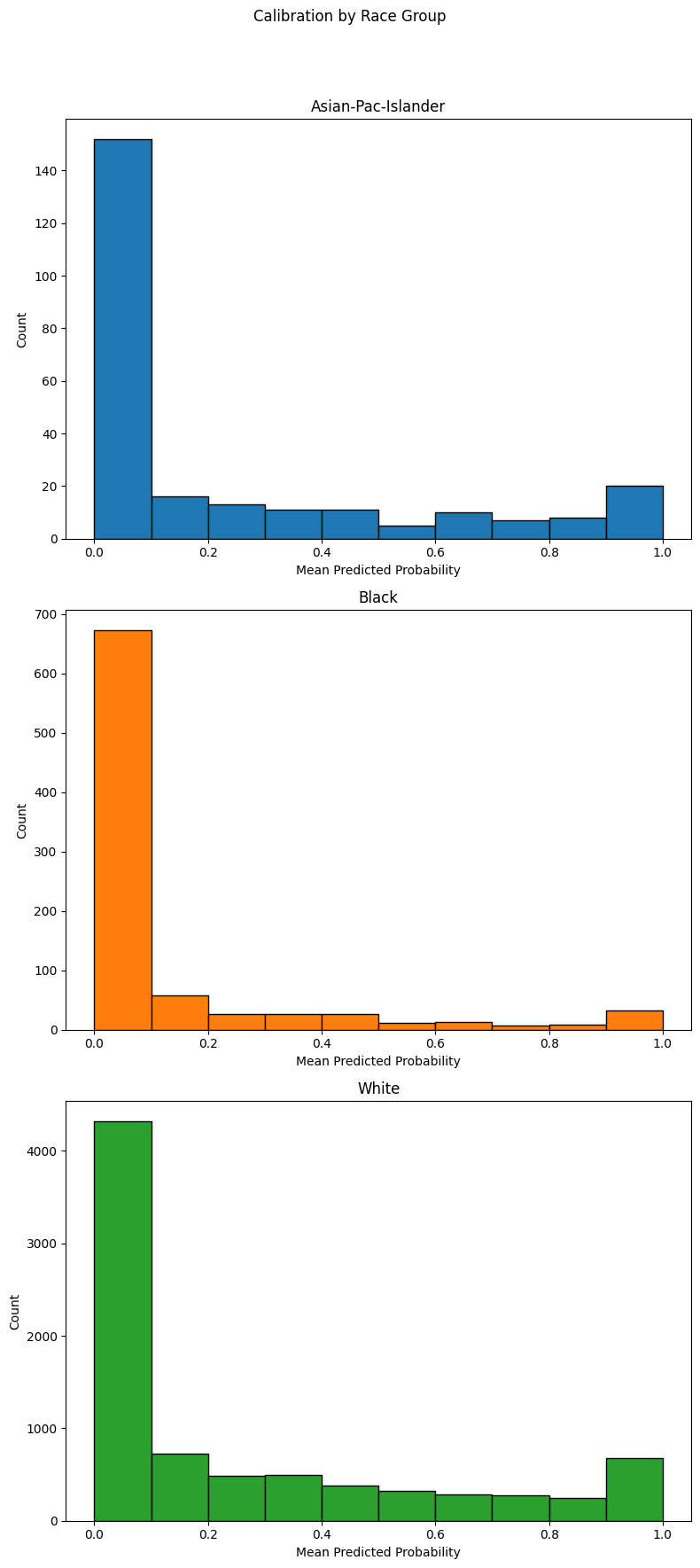
Calibration Curve with Histogram Overlay

The histogram bars at the base of the plot show how frequently predictions fall into each probability bin, grouped by demographic subgroup. This combined view helps validate whether deviations from the ideal diagonal are meaningful and well-supported by the underlying data.

For instance, if a group appears poorly calibrated in a region where very few predictions occur, the issue may be less impactful than one affecting densely populated bins. This visual diagnostic is especially valuable when auditing model behavior across real-world deployment scenarios.

Group Metrics Forest Plot

eq_plot_metrics_forest(group_metrics, metric_name, reference_group=None, figsize=(6, 4), save_path=None, filename='points_forest', sort_groups=True, ascending=True, title=None, statistical_tests=None)

Create a forest plot of point estimates for a specific metric across groups. Each group is plotted as a point along the horizontal axis, optionally compared against a reference group. Statistical significance markers can be displayed if test results are provided.

Parameters:

group_metrics (dict[str, dict[str, float]]) – Dictionary mapping group names to their metric values.
metric_name (str) – The metric to visualize (e.g., “Accuracy”, “AUC”).
reference_group (str or None) – Optional group name used as the vertical reference line in the plot.
figsize (tuple[float, float]) – Tuple for figure size (width, height).
save_path (str or None) – Directory path where the plot should be saved. If None, the plot is shown.
filename (str) – Filename for saving the plot (without extension).
sort_groups (bool) – Whether to sort groups by their metric values.
ascending (bool) – Sort order for groups if sorting is enabled.
title (str or None) – Optional custom title for the plot. If None, a default is generated.
statistical_tests (dict or None) – Dictionary mapping groups or omnibus test results to significance flags.

Important

The metric_name parameter can be set to any metric returned by eq.get_metrics() after slicing by a sensitive attribute (see Step 2: Slice Groups and Compute Point Estimates).

Available metrics: 'Accuracy', 'Precision', 'Recall', 'F1 Score', 'Specificity', 'TP Rate', 'FP Rate', 'FN Rate', 'TN Rate', 'TP', 'FP', 'FN', 'TN', 'Prevalence', 'Predicted Prevalence', 'ROC AUC', 'Average Precision Score', 'Log Loss', 'Brier Score', 'Calibration AUC'.

In practice, pass any of these from race_metrics, sex_metrics, or any subgroup dictionary produced by eq.get_metrics().

Once tests are computed, the eq_plot_metrics_forest function can visualize point estimates along with statistical annotations:

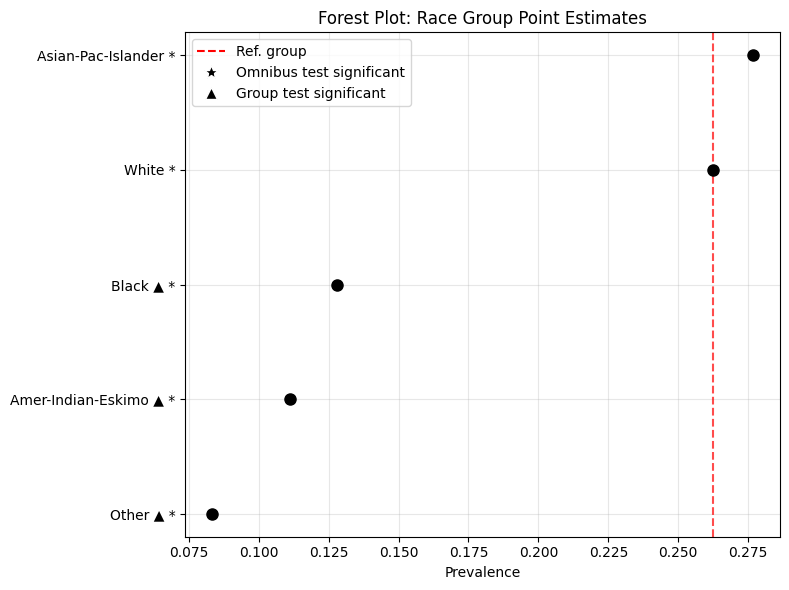
Example 1: Prevalance

eqb.eq_plot_metrics_forest(
    group_metrics=race_metrics,
    metric_name="Prevalence",
    title="Forest Plot: Race Group Point Estimates",
    reference_group="White",
    figsize=(8, 6),
    sort_groups=True,
    ascending=False,
    statistical_tests=stat_test_results_race,
)

Output

Effect Size

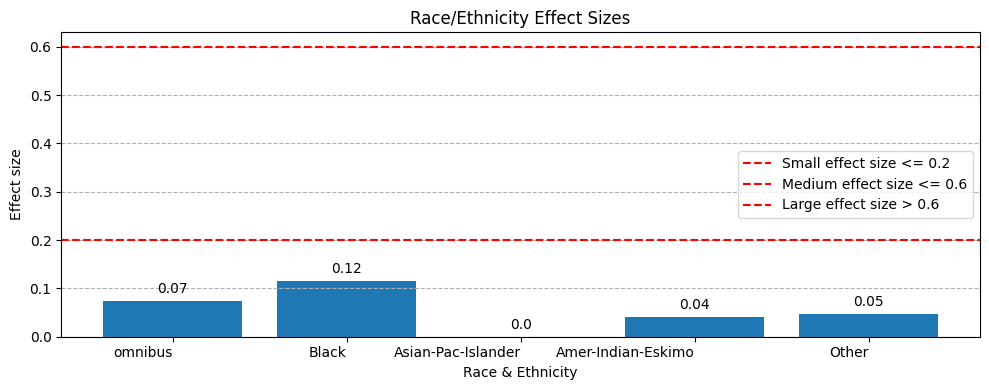
EquiBoots also calculates effect size when working with point estimates. Effect size helps quantify the strength of the relationship or difference, beyond just whether it is statistically significant. For example, in one analysis we observed that all effect sizes were low (under 0.2), with the highest being 0.11. This suggests that while statistical significance was found, the findings were not necessarily strong.

According to IBM Cognos documentation, for Cramer’s V:

ES ≤ 0.2 is interpreted as a weak result.
0.2 < ES ≤ 0.6 is interpreted as a moderate result.
ES > 0.6 is interpreted as a strong result.

plot_effect_sizes(stat_test_results, xlabel='Category', ylabel='Effect size', title='Effect Sizes by Group', figsize=(8, 6), rotation=0, save_path=None, filename='effect_sizes')

Generate a bar chart of effect sizes by group. Bars are annotated with numeric values, and horizontal reference lines are added at 0.2 and 0.6 to guide interpretation (weak, moderate, strong).

Parameters:

stat_test_results (dict[str, object]) – Mapping of group/category names to statistical test result objects containing .effect_size attributes.
xlabel (str) – Label for the x-axis.
ylabel (str) – Label for the y-axis.
title (str) – Title of the plot.
figsize (tuple[float, float]) – Tuple specifying figure size (width, height).
rotation (int) – Angle (in degrees) to rotate x-axis labels.
save_path (str or None) – Directory path where the plot should be saved. If None, the plot is shown.
filename (str) – Filename for saving the plot (without extension).

Example

from equiboots import plot_effect_sizes

# Assume stat_results is a dict of group -> test results with .effect_size
plot_effect_sizes(
    stat_test_results=stat_results,
    xlabel="Attribute",
    ylabel="Effect size",
    title="Effect Sizes by Group",
    figsize=(8, 6),
    rotation=30,
    save_path="./images",
    filename="effect_sizes_demo"
)

Output

Residual-Based Point Estimates

In regression tasks, residuals represent the difference between observed values and model predictions. A detailed explanation of the underlying formulas and metrics is provided in the regression residuals section of the Mathemtical Framework.

To visualize how these residuals vary across sensitive groups (e.g., race, sex, age group), you can use the following function:

eq_plot_residuals_by_group(data, alpha=0.6, show_centroids=False, title='Residuals by Group', filename='residuals_by_group', save_path=None, figsize=(8, 6), dpi=100, subplots=False, n_cols=2, n_rows=None, group=None, color_by_group=True, exclude_groups=0, show_grid=True)

Plot residuals grouped by subgroup.

This function visualizes regression residuals (i.e., the difference between actual and predicted values) across sensitive or analytical subgroups. It accepts a dictionary of group-level data and plots residual distributions, optionally showing centroids or overlaying all groups.

Parameters:

data (Dict[str, Dict[str, np.ndarray]]) – Dictionary of the form {group: {'y_true': ..., 'y_pred': ...}} or {group: {'y_actual': ..., 'y_prob': ...}} depending on the naming convention used.
alpha (float) – Transparency level for residual points (0.0 to 1.0).
show_centroids (bool) – Whether to display centroid markers for each group’s residuals.
title (str) – Title of the overall plot.
filename (str) – Base name for saving the figure.
save_path (Optional[str]) – Directory where the figure should be saved. If None, the figure is not saved.
figsize (Tuple[float, float]) – Width and height of the figure in inches.
dpi (int) – Resolution of the plot in dots per inch.
subplots (bool) – Whether to plot each group in a separate subplot.
n_cols (int) – Number of columns when using subplots.
n_rows (Optional[int]) – Number of rows when using subplots. If None, rows are auto-computed.
group (Optional[str]) – If specified, only this group will be plotted (subplots must be False).
color_by_group (bool) – Whether to assign colors uniquely per group.
exclude_groups (Union[int, str, List[str], Set[str]]) – Group(s) to exclude from the plot. Can be a single value or a list/set.
show_grid (bool) – Whether to display a background grid on each axis.

Returns:

None

Note

You can toggle centroid markers using the show_centroids parameter. When show_centroids=True, a centroid marker is added for each group to indicate the average residual. This helps identify whether a group is systematically over- or under-predicted. Centroids offer directional insight but do not reflect the full distribution or spread of residuals within a group.

This section demonstrates how to visualize group-level residuals using the eq_plot_residuals_by_group() function from the EquiBoots package.

We use the UCI Student Performance dataset [2], which contains academic, demographic, and behavioral data from Portuguese secondary school students. The goal is to evaluate how model residuals vary across sensitive groups when predicting final grades using a linear regression model.

Example 1: Residuals by Age Group (Overlayed)

The following example shows residuals plotted across age groups in a single overlayed axis. This allows for visual comparison of prediction errors across subgroups, with centroids included to indicate average residual positions.

eqb.eq_plot_residuals_by_group(
    data=sliced_age_data,
    title="Residuals by Age Group",
    color_by_group=True,
    figsize=(8, 6),
    show_centroids=True,
    show_grid=False,
)

Output

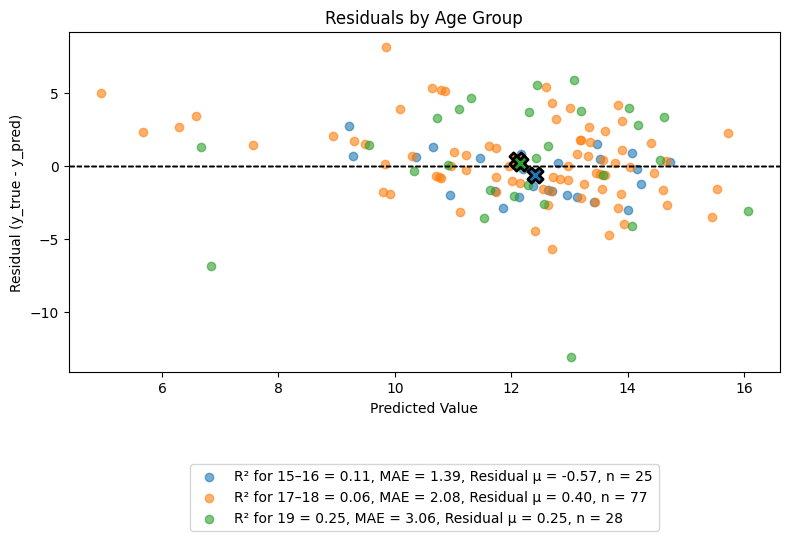
The output shows all groups together for side-by-side visual inspection of error spread and potential bias. To separate groups into distinct plots, use subplots=True.

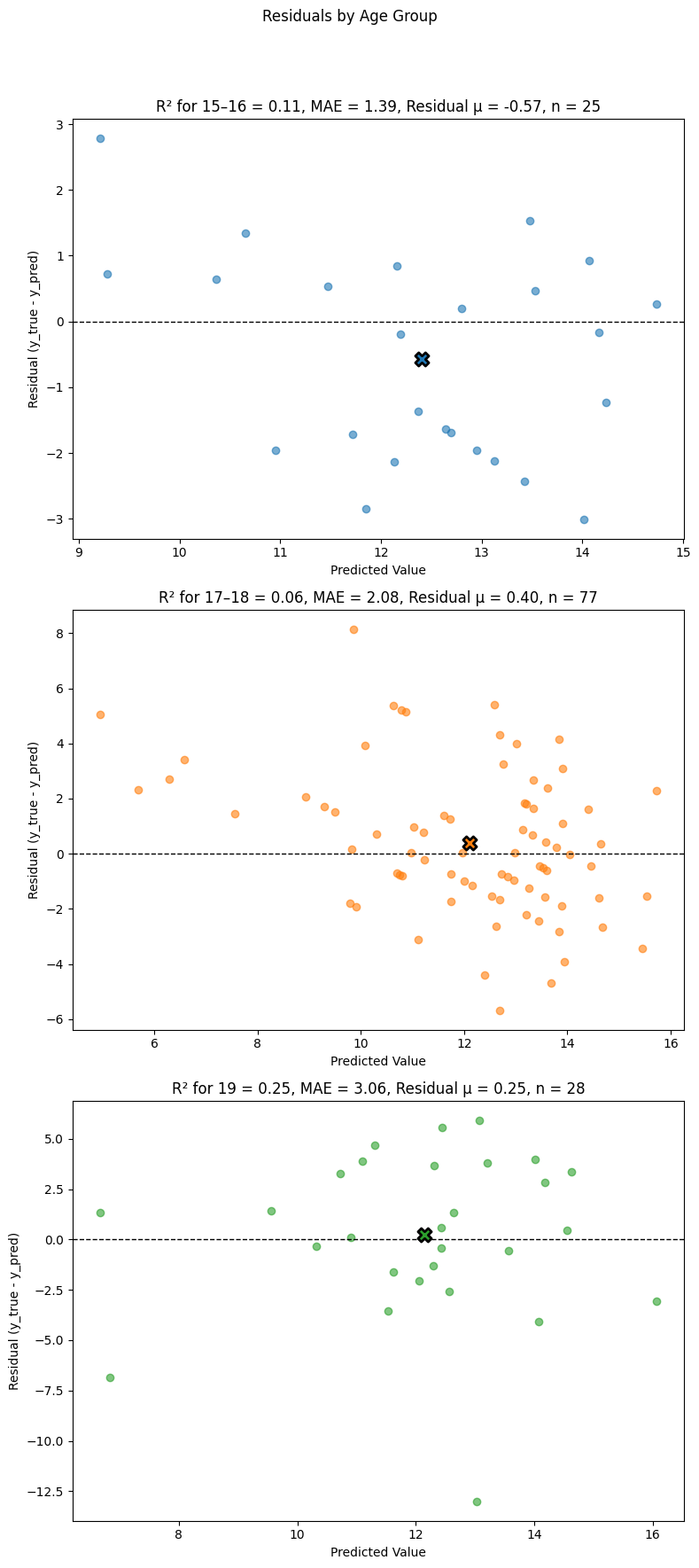
Example 2: Residuals by Age Group (Subplots)

In this example, we create separate subplots for each age group to facilitate individual analysis. This is particularly useful when the number of groups is large, as it prevents overcrowding in a single plot.

eqb.eq_plot_residuals_by_group(
    data=sliced_age_data,
    title="Residuals by Age Group (Subplots)",
    color_by_group=True,
    figsize=(12, 8),
    show_centroids=True,
    show_grid=False,
    subplots=True,
    n_cols=2,
    n_rows=2,
)

Output

Regression Residuals by Age Group (Subplots)

The output displays each age group’s residuals in its own subplot, allowing for a more granular examination of prediction errors. This layout can help identify specific groups that may require further investigation or targeted interventions.