Zero Variance Columns
Important
Ensure that your feature set X is free of zero-variance columns before using this method.
Zero-variance columns can lead to issues such as UserWarning: Features[feat_num] are constant
and RuntimeWarning: invalid value encountered in divide f = msb/msw during the model training process.
To check for and remove zero-variance columns, you can use the following code:
# Check for zero-variance columns and drop them
zero_variance_columns = X.columns[X.var() == 0]
if not zero_variance_columns.empty:
X = X.drop(columns=zero_variance_columns)
Zero-variance columns in the feature set \(X\) refer to columns where all values are identical. Mathematically, if \(X_j\) is a column in \(X\), the variance of this column is calculated as:
where \(X_{ij}\) is the \(i\)-th observation of feature \(j\), and \(\bar{X}_j\) is the mean of the \(j\)-th feature. Since all \(X_{ij}\) are equal, \(\text{Var}(X_j)\) is zero.
Effects on Model Training
UserWarning:
During model training, algorithms often check for variability in features to determine their usefulness in predicting the target variable. A zero-variance column provides no information, leading to the following warning:
UserWarning: Features[feat_num] are constant
This indicates that the feature \(X_j\) has no variability and, therefore, cannot contribute to the model’s predictive power.
RuntimeWarning:
When calculating metrics like the F-statistic used in Analysis of Variance (ANOVA) or feature importance metrics, the following ratio is computed:
\[F = \frac{\text{MSB}}{\text{MSW}}\]where \(\text{MSB}\) (Mean Square Between) and \(\text{MSW}\) (Mean Square Within) are defined as:
\[\text{MSB} = \frac{1}{k-1} \sum_{j=1}^{k} n_j (\bar{X}_j - \bar{X})^2\]\[\text{MSW} = \frac{1}{n-k} \sum_{j=1}^{k} \sum_{i=1}^{n_j} (X_{ij} - \bar{X}_j)^2\]If \(X_j\) is a zero-variance column, then \(\text{MSW} = 0\) because all \(X_{ij}\) are equal to \(\bar{X}_j\). This leads to a division by zero in the calculation of \(F\):
\[F = \frac{\text{MSB}}{0} \rightarrow \text{undefined}\]which triggers a runtime warning:
RuntimeWarning: invalid value encountered in divide f = msb/msw
indicating that the calculation involves dividing by zero, resulting in undefined or infinite values.
To avoid these issues, ensure that zero-variance columns are removed from \(X\) before proceeding with model training.
Dependent Variable
Important
Additionally, ensure that y (the target variable) is passed as a Series and not as a DataFrame.
Passing y as a DataFrame can cause issues such as DataConversionWarning: A column-vector y was passed
when a 1d array was expected. Please change the shape of y to (n_samples,).
If y is a DataFrame, you can convert it to a Series using the following code:
# Convert y to a Series if it's a DataFrame
if isinstance(y, pd.DataFrame):
y = y.squeeze()
This conversion ensures that the target variable y has the correct shape, preventing the aforementioned warning.
Target Variable Shape and Its Effects
The target variable \(y\) should be passed as a 1-dimensional array (Series) and not as a 2-dimensional array (DataFrame). If \(y\) is passed as a DataFrame, the model training process might raise the following warning:
DataConversionWarning: A column-vector y was passed when a 1d array was expected.
Please change the shape of y to (n_samples,).
Explanation:
Machine learning models generally expect the target variable \(y\) to be in the shape of a 1-dimensional array, denoted as \(y = \{y_1, y_2, \dots, y_n\}\), where \(n\) is the number of samples. Mathematically, \(y\) is represented as:
When \(y\) is passed as a DataFrame, it is treated as a 2-dimensional array, which has the form:
or
where each sample is represented as a column vector. This discrepancy in dimensionality can cause the model to misinterpret the data,
leading to the DataConversionWarning.
Solution
To ensure \(y\) is interpreted correctly as a 1-dimensional array, it should be passed as a Series. If \(y\) is currently a DataFrame, you can convert it to a Series using the following code:
# Convert y to a Series if it's a DataFrame
if isinstance(y, pd.DataFrame):
y = y.squeeze()
The method squeeze() effectively removes any unnecessary dimensions, converting a 2-dimensional DataFrame
with a single column into a 1-dimensional Series. This ensures that \(y\) has the correct shape, preventing
the aforementioned warning and ensuring the model processes the target variable correctly.
Scaling Before Imputation
Important
It is crucial to apply scaling before imputation during the data preprocessing pipeline to preserve the mathematical integrity of the transformations and ensure accurate imputations. The correct sequence for the pipeline is as follows:
pipeline_steps = [
("Scaler", StandardScaler()),
("Imputer", SimpleImputer()),
]
Accurate Imputation with Normalized Data
Imputation methods, such as mean, median, or k-Nearest Neighbors (k-NN), depend on the scale of the data. Without scaling, features with large magnitudes can disproportionately influence the imputed values, especially in methods like k-NN imputation.
For example, consider a feature \(X = [1, 2, \text{NaN}, 4, 1000]\) with a missing value. The high value of 1000 significantly skews the mean, \(\mu = \frac{1 + 2 + 4 + 1000}{4} = 251.75\), leading to an imputed value of 251.75, which does not reflect the underlying data pattern.
If scaling is applied first, the data becomes:
Now, imputing the missing value using the scaled data results in a more accurate representation of the data’s distribution. Once the scaling is reversed, the imputed value aligns more naturally with the original data.
Consistency in Data Transformation
Scaling before imputation ensures that the transformations applied are consistent across the entire dataset, including the imputed values. For instance, consider a feature \(X = [1, 2, \text{NaN}, 4, 5]\). After applying standardization first, the available values are transformed using:
where \(\mu\) and \(\sigma\) are calculated using only the non-missing values. The imputed values are then calculated on this standardized scale, maintaining consistency in both the transformation and the imputation process.
Had imputation been applied first, the calculated mean and standard deviation would have been skewed by the imputed value, potentially leading to an inaccurate scaling transformation.
Prevention of Imputation Bias
By scaling first, we mitigate the risk of imputing values that disproportionately align with features of larger magnitudes. For instance, in datasets where features vary widely in scale, imputing before scaling might introduce a bias in imputed values that heavily favors dominant features. Scaling ensures that all features are on an equal footing prior to imputation.
Avoiding Distortions in Nearest Neighbor Imputation
-Nearest Neighbors (k-NN) imputation relies on the calculation of distances between data points. If features are not scaled beforehand, large-magnitude features dominate the distance calculations, resulting in imputation values that may not reflect the true proximity of data points. Scaling first ensures that each feature contributes equally to the distance metric.
For example, consider two features:
\(\text{Feature1} = [1, 2, \text{NaN}, 4]\) and \(\text{Feature2} = [100, 200, \text{NaN}, 400]\).
Without scaling, the distance calculation is dominated by Feature2 due to its larger magnitude. Scaling the features first eliminates this bias, leading to more meaningful imputations.
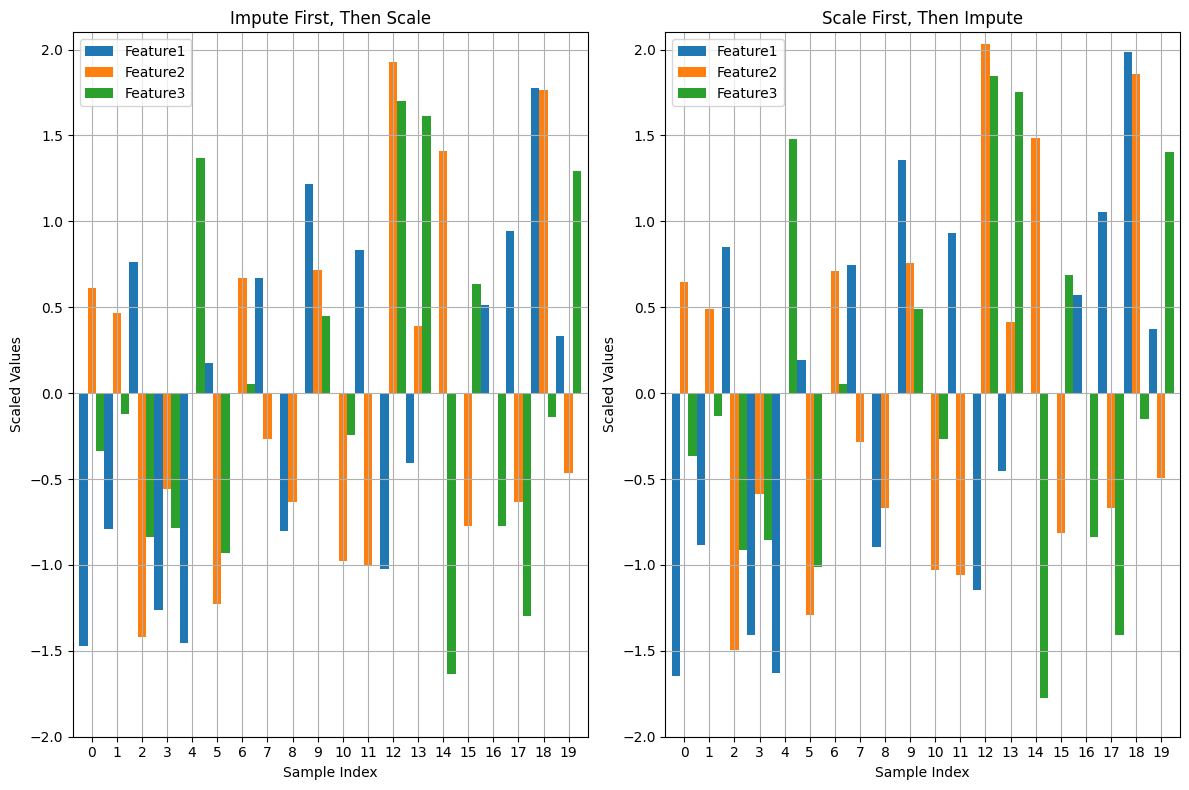
Visual Proof
The accompanying figure demonstrates the difference between the two approaches:
Left Panel (Impute First, Then Scale): Notice the irregular distribution of scaled values after imputation, with some features exhibiting unnatural spikes.
Right Panel (Scale First, Then Impute): Displays a more uniform and consistent distribution across features, reflecting the integrity of the scaled data.
This highlights that scaling before imputation results in a cleaner, more consistent preprocessing pipeline.
Column Stratification with Cross-Validation
Important
Using stratify_cols with Cross-Validation
It is important to note that stratify_cols cannot be used when performing cross-validation.
Cross-validation involves repeatedly splitting the dataset into training and validation sets to
evaluate the model’s performance across different subsets of the data.
Explanation:
When using cross-validation, the process automatically handles the stratification of the target variable \(y\),
if specified. This ensures that each fold is representative of the overall distribution of \(y\). However,
stratify_cols is designed to stratify based on specific columns in the feature set \(X\), which can lead to
inconsistencies or even errors when applied in the context of cross-validation.
Since cross-validation inherently handles stratification based on the target variable, attempting to apply additional stratification based on specific columns would conflict with the cross-validation process. This can result in unpredictable behavior or failure of the cross-validation routine.
However, you can use stratify_y during cross-validation to ensure that each fold of the dataset is representative
of the distribution of the target variable \(y\). This is a common practice to maintain consistency in the distribution
of the target variable across the different training and validation sets.
Cross-Validation and Stratification
Let \(D = \{(X_i, y_i)\}_{i=1}^n\) be the dataset with \(n\) samples, where \(X_i\) is the feature set and \(y_i\) is the target variable.
In k-fold cross-validation, the dataset \(D\) is split into \(k\) folds \(\{D_1, D_2, \dots, D_k\}\).
When stratifying by \(y\) using stratify_y, each fold \(D_j\) is constructed such that the distribution of \(y\) in each fold is similar to the distribution of \(y\) in \(D\).
Mathematically, if \(P(y=c)\) is the probability of the target variable \(y\) taking on class \(c\), then:
for all folds \(D_j\) and all classes \(c\).
This ensures that the stratified folds preserve the same class proportions as the original dataset.
On the other hand, stratify_cols stratifies based on specific columns of \(X\). However, in cross-validation, the primary focus is on the target variable \(y\).
Attempting to stratify based on \(X\) columns during cross-validation can disrupt the process of ensuring a representative sample of \(y\) in each fold. This can lead to unreliable performance estimates and, in some cases, errors.
Therefore, the use of stratify_y is recommended during cross-validation to maintain consistency in the target variable distribution across folds, while stratify_cols should be avoided.
Model Calibration
Model calibration refers to the process of adjusting the predicted probabilities of a model so that they more accurately reflect the true likelihood of outcomes. This is crucial in machine learning, particularly for classification problems where the model outputs probabilities rather than just class labels.
Goal of Calibration
The goal of calibration is to ensure that the predicted probability \(\hat{p}(x)\) is equal to the true probability that \(y = 1\) given \(x\). Mathematically, this can be expressed as:
This equation states that for all instances where the model predicts a probability \(p\), the true fraction of positive cases should also be \(p\).
Calibration Curve
To assess calibration, we often use a calibration curve. This involves:
Binning the predicted probabilities \(\hat{p}(x)\) into intervals (e.g., [0.0, 0.1), [0.1, 0.2), …, [0.9, 1.0]).
Calculating the mean predicted probability \(\hat{p}_i\) for each bin \(i\).
Calculating the empirical frequency \(f_i\) (the fraction of positives) in each bin.
For a perfectly calibrated model:
Brier Score
The Brier score is one way to measure the calibration of a model. It’s calculated as:
Where:
\(N\) is the number of instances.
\(\hat{p}(x_i)\) is the predicted probability for instance \(i\).
\(y_i\) is the actual label for instance \(i\) (0 or 1).
The Brier score penalizes predictions that are far from the true outcome. A lower Brier score indicates better calibration and accuracy.
Platt Scaling
One common method to calibrate a model is Platt Scaling. This involves fitting a logistic regression model to the predictions of the original model. The logistic regression model adjusts the raw predictions \(\hat{p}(x)\) to output calibrated probabilities.
Mathematically, Platt scaling is expressed as:
Where \(A\) and \(B\) are parameters learned from the data. These parameters adjust the original probability estimates to better align with the true probabilities.
Isotonic Regression
Another method is Isotonic Regression, a non-parametric approach that fits a piecewise constant function. Unlike Platt Scaling, which assumes a logistic function, Isotonic Regression only assumes that the function is monotonically increasing. The goal is to find a set of probabilities \(p_i\) that are as close as possible to the true probabilities while maintaining a monotonic relationship.
The isotonic regression problem can be formulated as:
Where \(p_i\) are the adjusted probabilities, and the constraint ensures that the probabilities are non-decreasing.
Example: Calibration in Logistic Regression
In a standard logistic regression model, the predicted probability is given by:
Where \(w\) is the vector of weights, and \(x\) is the input feature vector.
If this model is well-calibrated, \(\hat{p}(x)\) should closely match the true conditional probability \(P(y = 1 \mid x)\). If not, techniques like Platt Scaling or Isotonic Regression can be applied to adjust \(\hat{p}(x)\) to be more accurate.
Summary
Model calibration is about aligning predicted probabilities with actual outcomes.
Mathematically, calibration ensures \(\hat{p}(x) = P(y = 1 \mid \hat{p}(x) = p)\).
Platt Scaling and Isotonic Regression are two common methods to achieve calibration.
Brier Score is a metric that captures both the calibration and accuracy of probabilistic predictions.
Calibration is essential when the probabilities output by a model need to be trusted, such as in risk assessment, medical diagnosis, and other critical applications.
Using Imputation and Scaling in Pipeline Steps for Model Preprocessing
The pipeline_steps parameter accepts a list of tuples, where each tuple specifies
a transformation step to be applied to the data. For example, the code block below
performs imputation followed by standardization on the dataset before training the model.
pipeline_steps=[
("Imputer", SimpleImputer()),
("StandardScaler", StandardScaler()),
]
When Is Imputation and Feature Scaling in pipeline_steps Beneficial?
Logistic Regression: Highly sensitive to feature scaling and missing data. Preprocessing steps like imputation and standardization improve model performance significantly.
Linear Models (e.g., Ridge, Lasso): Similar to Logistic Regression, these models require feature scaling for optimal performance.
SVMs: Sensitive to the scale of the features, requiring preprocessing like standardization.
Models Not Benefiting From Imputation and Scaling in pipeline_steps
Tree-Based Models (e.g., XGBoost, Random Forests, Decision Trees): These models are invariant to feature scaling and can handle missing values natively. Passing preprocessing steps like StandardScaler or Imputer may be redundant or even unnecessary.
Why Doesn’t XGBoost Require Imputation and Scaling in pipeline_steps?
XGBoost and similar tree-based models work on feature splits rather than feature values directly. This makes them robust to unscaled data and capable of handling missing values using default mechanisms like missing parameter handling in XGBoost. Thus, adding steps like scaling or imputation often does not improve and might complicate the training process.
To this end, it is best to use pipeline_steps strategically for algorithms that rely on numerical properties (e.g., Logistic Regression). For XGBoost, focus on other optimization techniques like hyperparameter tuning and feature engineering instead.
Caveats in Imbalanced Learning
Working with imbalanced datasets introduces several challenges that must be carefully addressed to ensure model performance is both effective and fair. Below are key caveats to consider:
Bias from Class Distribution
In imbalanced datasets, the prior probabilities of the classes are highly skewed:
This imbalance can lead models to prioritize the majority class, resulting in biased predictions that overlook the minority class. Models may optimize for accuracy but fail to capture the true distribution of minority class instances.
Threshold-Dependent Predictions
Many classifiers rely on a decision threshold \(\tau\) to make predictions:
With imbalanced data, the default threshold may favor the majority class, causing a high rate of false negatives for the minority class. Adjusting the threshold to account for imbalance can help mitigate this issue, but it requires careful tuning and validation.
Limitations of Accuracy
Traditional accuracy is a misleading metric in imbalanced datasets. For example, a model predicting only the majority class can achieve high accuracy despite failing to identify any minority class instances. Instead, alternative metrics should be used:
Precision for the minority class:
Measures the proportion of correctly predicted minority class instances out of all instances predicted as the minority class.
\[\text{Precision} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}}\]
Recall for the minority class:
Measures the proportion of correctly predicted minority class instances out of all actual minority class instances.
\[\text{Recall} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}}\]
F1-Score, the harmonic mean of precision and recall:
Balances precision and recall to provide a single performance measure.
\[F1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\]ROC AUC (Receiver Operating Characteristic - Area Under the Curve):
Measures the model’s ability to distinguish between classes. It is the area under the ROC curve, which plots the True Positive Rate (Recall) against the False Positive Rate.
\[\text{True Positive Rate (TPR)} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}}\]\[\text{False Positive Rate (FPR)} = \frac{\text{False Positives}}{\text{False Positives} + \text{True Negatives}}\]
The AUC (Area Under Curve) is computed by integrating the ROC curve:
\[\text{AUC} = \int_{0}^{1} \text{TPR}(\text{FPR}) \, d(\text{FPR})\]This integral represents the total area under the ROC curve, where:
A value of 0.5 indicates random guessing.
A value of 1.0 indicates a perfect classifier.
Practically, the AUC is estimated using numerical integration techniques such as the trapezoidal rule over the discrete points of the ROC curve.
Integration and Practical Considerations
The ROC AUC provides an aggregate measure of model performance across all classification thresholds.
However:
Imbalanced Datasets: The ROC AUC may still appear high if the classifier performs well on the majority class, even if the minority class is poorly predicted. In such cases, metrics like Precision-Recall AUC are more informative.
Numerical Estimation: Most implementations (e.g., in scikit-learn) compute the AUC numerically, ensuring fast and accurate computation.
These metrics provide a more balanced evaluation of model performance on imbalanced datasets. By using metrics like ROC AUC in conjunction with precision, recall, and F1-score, practitioners can better assess a model’s effectiveness in handling imbalanced data.
Impact of Resampling Techniques
Resampling methods such as oversampling and undersampling can address class imbalance but come with trade-offs:
Oversampling Caveats
Methods like SMOTE may introduce synthetic data that does not fully reflect the true distribution of the minority class.
Overfitting to the minority class is a risk if too much synthetic data is added.
Undersampling Caveats
Removing samples from the majority class can lead to loss of important information, reducing the model’s generalizability.
SMOTE: A Mathematical Illustration
SMOTE (Synthetic Minority Over-sampling Technique) is a widely used algorithm for addressing class imbalance by generating synthetic samples for the minority class. However, while powerful, SMOTE comes with inherent caveats that practitioners should understand. Below is a mathematical illustration highlighting these caveats.
Synthetic Sample Generation
SMOTE generates synthetic samples by interpolating between a minority class sample and its nearest neighbors. Mathematically, a synthetic sample \(x_{synthetic}\) is defined as:
where:
\(\mathbf{x}_i\): A minority class sample.
\(\mathbf{x}_k\): One of its \(k\) nearest neighbors (from the same class).
\(\delta\): A random value drawn from a uniform distribution, \(\delta \sim U(0, 1)\).
This process ensures that synthetic samples are generated along the line segments connecting minority class samples and their neighbors.
Caveats in Application
Overlapping Classes:
SMOTE assumes that the minority class samples are well-clustered and separable from the majority class.
If the minority class overlaps significantly with the majority class, synthetic samples may fall into regions dominated by the majority class, leading to misclassification.
Noise Sensitivity:
SMOTE generates synthetic samples based on existing minority class samples, including noisy or mislabeled ones.
Synthetic samples created from noisy data can amplify the noise, degrading model performance.
Feature Space Assumptions:
SMOTE relies on linear interpolation in the feature space, which assumes that the feature space is homogeneous.
In highly non-linear spaces, this assumption may not hold, leading to unrealistic synthetic samples.
Dimensionality Challenges:
In high-dimensional spaces, nearest neighbor calculations may become less meaningful due to the curse of dimensionality.
Synthetic samples may not adequately represent the true distribution of the minority class.
Risk of Overfitting:
If SMOTE is applied excessively, the model may overfit to the synthetic minority class samples, reducing generalizability to unseen data.
Example of Synthetic Sample Creation
To illustrate, consider a minority class sample \(f{x}_i = [1, 2]\) and its nearest neighbor \(f{x}_k = [3, 4]\). If \(\delta = 0.5\), the synthetic sample is computed as:
This synthetic sample lies midway between the two points in the feature space.
Mitigating the Caveats
Combine SMOTE with Undersampling: Techniques like
SMOTEENNorSMOTETomekremove noisy or overlapping samples after synthetic generation.Apply with Feature Engineering: Ensure the feature space is meaningful and represents the underlying data structure.
Tune Oversampling Ratio: Avoid generating excessive synthetic samples to reduce overfitting.
Threshold Tuning Considerations
Mathematical Basis:
In binary classification, the decision rule is represented as:
Here:
\(P(\text{positive class} \mid X)\) is the predicted probability of the positive class given features \(X\).
\(\tau\) is the threshold value, which determines the decision boundary.
By default, \(\tau = 0.5\), but this may not always align with the desired balance between precision and recall.
The Precision-Recall Tradeoff
When tuning the threshold \(\tau\), it is important to recognize its impact on precision and recall:
Precision increases as \(\tau\) increases, since the model becomes more conservative in predicting the positive class, reducing false positives.
Recall decreases as \(\tau\) increases, as the model’s stricter criteria result in more false negatives.
This tradeoff is especially critical in domains where false positives or false negatives have significantly different costs, such as:
Medical diagnostics: Emphasize recall to minimize false negatives.
Spam detection: Emphasize precision to reduce false positives.
Threshold Optimization
Adjusting the threshold based solely on a single metric (e.g., maximizing precision) may lead to suboptimal performance in other metrics. For example:
Increasing \(\tau\) to improve precision might drastically reduce recall.
Decreasing \(\tau\) to maximize recall might result in an unacceptably high false positive rate.
A balanced metric like the F-beta score can address this tradeoff:
Here, \(\beta\) adjusts the weight given to recall relative to precision:
\(\beta > 1\): Recall is prioritized.
\(\beta < 1\): Precision is prioritized.
ElasticNet Regularization
Elastic net minimizes the following cost function:
where:
\(\|\beta\|_1 = \sum_{j=1}^p |\beta_j|\) represents the \(L1\) norm, promoting sparsity.
\(\|\beta\|_2^2 = \sum_{j=1}^p \beta_j^2\) represents the \(L2\) norm, promoting shrinkage.
\(\lambda\) controls the regularization strength.
\(\alpha \in [0, 1]\) determines the balance between the \(L1\) and \(L2\) penalties.
Important Considerations
Balance of Sparsity and Shrinkage:
\(\alpha = 1\): Reduces to Lasso (\(L1\) only).
\(\alpha = 0\): Reduces to Ridge (\(L2\) only).
Intermediate values allow elastic net to select features while managing multicollinearity.
Regularization Strength:
Larger \(\lambda\) increases bias but reduces variance, favoring simpler models.
Smaller \(\lambda\) reduces bias but may increase variance, allowing more complex models.
Feature Correlation:
Elastic net handles correlated features better than Lasso, spreading coefficients across groups of related predictors.
Hyperparameter Tuning:
Both \(\alpha\) and \(\lambda\) should be optimized via cross-validation to achieve the best performance.
Elastic net is well-suited for datasets with mixed feature relevance, reducing overfitting while retaining important predictors.
Important
When combining elastic net with RFE, it is important to note that the recursive process may interact with the regularization in elastic net.
Elastic net’s built-in feature selection can prioritize sparsity, but RFE explicitly removes features step-by-step. This may lead to redundancy in feature selection efforts or alter the balance between \(L1\) and \(L2\) penalties as features are eliminated.
Careful calibration of \(\alpha\) and \(\lambda\) is essential when using RFE alongside elastic net to prevent over-penalization or premature exclusion of relevant features.
CatBoost Training Parameters
According to the CatBoost documentation:
“For the Python package several parameters have aliases. For example, the –iterations parameter has the following synonyms: num_boost_round, n_estimators, num_trees. Simultaneous usage of different names of one parameter raises an error.”
Important
Attempting to pass more than one of these synonymous hyperparameters will result in the following error:
CatBoostError: only one of the parameters iterations, n_estimators, num_boost_round, num_trees should be initialized.
To prevent this issue, ensure you define only one of these parameters (e.g., n_estimators) in your configuration, and avoid including any other aliases such as iterations or num_boost_round.
Example: Tuning hyperparameters for CatBoost
When defining hyperparameters for grid search, specify only one alias in your configuration. Below is an example:
cat = CatBoostClassifier(
n_estimators=100, ## num estimator/iteration/boostrounds
learning_rate=0.1,
depth=6,
loss_function="Logloss",
)
tuned_hyperparameters_cat = {
f"{cat_name}__n_estimators": [1500],
## Additional hyperparameters
f"{cat_name}__learning_rate": [0.01, 0.1],
f"{cat_name}__depth": [4, 6, 8],
f"{cat_name}__loss_function": ["Logloss"],
}
This ensures compatibility with CatBoost’s requirements and avoids errors during hyperparameter tuning.